論理関数とその応用
第三部
この教科書はBookletを利用して作成している。
本書の見方
- ページをめくる
- 左(右)ページの左(右)端クリックまたはドラッグする
左(右)矢印キーを押す - 1ページ分の移動
- 左右上端にある[Next]、[Previous]タブをクリックする
- 章の頭に移動
- 右上の【章の移動】タブをクリックし、現れた章を選ぶ
- ページのジャンプ
- 右上のページ番号表示タブをクリックし、現れたページを選ぶ
- 画像の拡大およびリンク先への移動
- 画像やリンク先をクリックすれば、別ウィンドウ(タブ)で表示される
目 次
第三部- 5章 有限オートマトンの理論
-
文字列と言語
有限オートマトン
正則関数
正則集合
- 6章 論理関数族の理論
-
閉関数族
完全性
第二部
- 3章 論理関数
-
論理関数の定義
排他的論理和に関する公式
標準形
標準形の求め方
論理式の簡単化 - 4章 順序回路
-
順序回路とは
状態の符号化
第一部
- 0章 学習の指針
- 1章 論理と集合
-
集合の記法
命題論理とその記法
1変数述語と集合
基本等式
基本不等式
双対原理
公式の証明 - 2章 論理回路
-
AND、OR、NOT素子
論理式(回路)の設計
加算器
集積回路の原理
第5章 有限オートマトンの理論
順序回路はどのような能力を持つ、即ち(原理的に)何ができて、何ができないのだろうか。順序回路では、入力、出力、状態(一時記憶)がすべて $0,\ 1$ で表されて(符号化されて)いる形で扱ったが、本節では、一旦 $0,\ 1$ から離れて、より一般的な枠組みのもとで、この問題を扱う。5.1節 文字列と言語
使われる文字の有限集合をアルファベットという。アルファベット $\Sigma$ 中の文字を($0$ 個以上)並べた列を $\Sigma$ 上の文字列といい、以下のような記法(定義)を用いる。| 名前 | 記法 | 定義・意味 | 備考 |
| 長さ | $|w|$ | 文字列 $w$ に出現する文字の個数 | $|aaba|=4$ |
| 空列 | $\varepsilon$ | 長さ $0$ の文字列 | |
| $\Sigma^+$ | $\Sigma$ 上の長さ $1$ 以上の文字列の集合 | $\{a,b\}^+=\{a,b,aa,ab,ba,bb,aaa,\cdots\}$ | |
| $\Sigma^*$ | $\Sigma$ 上の長さ $0$ 以上の文字列の集合 | $\Sigma^*=\Sigma^+\cup\{\varepsilon\}$ | |
| 連接 | $v\cdot w,\ vw$ | 文字列 $v$ の後に文字列 $w$ をつなげた文字列 | $aba\cdot bba=ababba,\ ab\varepsilon=\varepsilon ab=ab$ |
| ベキ | $w^n$ | 文字列 $w$ を $n$ 個つなげた文字列 | $(ab)^3=ababab,\ (ab)^0=\varepsilon$ |
アルファベット $\Sigma$ 上の文字列の集合 $L\subseteq \Sigma^*$ を $\Sigma$ 上の言語といい、以下のような記法(定義)を用いる。
| 名前 | 記法 | 定義・意味 | 備考 |
| 連接 | $KL$ | $KL:=\{vw\;|\;v\in K,\ w\in L\}$ | $\{ab,a\}\{\varepsilon,a,ba\}=\{ab,a,aba,aa,abba\}$ |
| ベキ | $L^n$ | $L^0:=\{\varepsilon\},\ L^{n+1}:=L^nL$ | $\{ab,a\}^3=\{ababab,ababa,abaab,abaa,aabab,aaba,aaab,aaa\}$ |
| 正閉包 | $L^+$ | $\displaystyle L^+:=\bigcup_{n=1}^\infty L^n$ | $\{a,ba\}^+=\{a,b,aa,aba,baa,baba,aaa,\cdots\}$ |
| 閉包 | $L^*$ | $\displaystyle L^*:=\bigcup_{n=0}^\infty L^n$ | $L^*=L^+\cup\{\varepsilon\},\ \{a,ba\}^*=\{\varepsilon,a,b,aa,aba,baa,baba,aaa,\cdots\}$ |
言語 $K,\,L,\,M\subseteq \Sigma^*$ に対し、以下が成立つ。(交換法則は成り立たない)
正則言語を上記の構成に従って表現するとき、煩雑さを避けるために集合を表す中括弧 $\{,\ \}$ を省略して、$\{\alpha\}$ を単に $\alpha$ と書く。このような表現を正則(正規)表現といい、広範囲の応用を持つ。
例.$(\{a\}\cup\{b\})^*\{ab\}=(a\cup b)^*ab$ は $ab$ で終わる $\{a,b\}$ 上の文字列の集合を表す。
| 結合則 | $K(LM)=(KL)M$ |
| 分配則 | $K(L\cup M)=KL\cup KM$ $(L\cup M)K=LK\cup MK$ |
| $K(L\cap M)\subseteq KL\cap KM$ $(L\cap M)K\subseteq LK\cap MK$ | |
| 閉包の式 | $L^*=L^*L^*=(L^*)^*=(L^*)^+=(L^+)^*=(L\cup\{\varepsilon\})^+$ |
| 正閉包の式 | $L^+=LL^*=L^*L=L^*L^+=L^+L^*=(L^+)^+$ |
| $(K\cup L)^*=(K^*L^*)^*=(K^*\cup L^*)^*$ | |
| $K^*L=K(K^*L)\cup L$ $KL^*=(KL^*)L\cup K$ |
| 問. |
|
5.2節 正則言語と正則(正規)表現
$\Sigma$ 上の正則言語を、次のように帰納的に定義する。- $\alpha \in \Sigma^*$ に対し、$\{\alpha\}$ は正則言語である。$\emptyset$ は正則言語である
- $K,L\subseteq \Sigma^*$ が正則言語ならば、$KL,\ K\cup L,\ K^*$ も正則言語である
- 1.2.で構成されるものだけが正則言語である
正則言語を上記の構成に従って表現するとき、煩雑さを避けるために集合を表す中括弧 $\{,\ \}$ を省略して、$\{\alpha\}$ を単に $\alpha$ と書く。このような表現を正則(正規)表現といい、広範囲の応用を持つ。
例.$(\{a\}\cup\{b\})^*\{ab\}=(a\cup b)^*ab$ は $ab$ で終わる $\{a,b\}$ 上の文字列の集合を表す。
| 問.$\Sigma=\{a,b\}$ 上の正則表現に関する次の問に答えよ。 |
|
5.3節 Mealy オートマトン
第4章で紹介した出力・状態遷移図で表されるシステムを Mealy オートマトン という。 形式的には、Mealy オートマトンは $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ で、- $S$ は状態の有限集合
- $\Sigma$ は入力文字の有限集合
- $\Gamma$ は出力文字の有限集合
- $s_0\in S$ は開始状態
- $\delta:S\times \Sigma\to S$ は状態遷移関数
- $\gamma:S\times \Sigma\to \Gamma$ は出力関数
Meallyオートマトンを図示するときは、状態は$\circled{ }$で、開始状態は$\Large\rhd$を付け${\Large\rhd}\circled{ }$で、状態遷移関数と出力関数は状態間のラベル付き矢印で $\transition{\;s\;}{a;\gamma(s,a)}\circled{\delta(s,a)}$ のように表す。
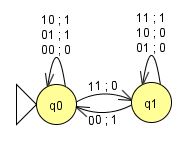
| 状態\入力 | $00$ | $01$ | $10$ | $11$ |
| $q_0$ | $q_0,0$ | $q_0,1$ | $q_0,1$ | $q_1,0$ |
| $q_1$ | $q_0,1$ | $q_1,0$ | $q_1,0$ | $q_1,1$ |
例.4.1節の同期式加算回路(右図)の場合、$A=(\{q_0,q_1\},\{00,01,10,11\},\{0,1\},q_0,\delta,\gamma)\ $で、状態遷移関数 $\delta$ および出力関数 $\gamma$ は右の表で与えられる。
| 実習.オートマトンシミュレータJFLAPを用いて、その動作を確認しよう。 |
|
5.4節 正則関数
Mealy オートマトンを解析するために、入力列に対し、その最終出力を与える関数を考えたい。そこで、$A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ とその状態 $s$ に対し、$\delta_s^*:\Sigma^*\to S,\ \gamma_s^+:\Sigma^+\to \Gamma$ を、$\begin{cases}\delta_s^*(\varepsilon):=s\\ \delta_s^*(\alpha a):=\delta(\delta_s^*(\alpha),a)\end{cases} \gamma_s^+(\alpha a):=\gamma(\delta_s^*(\alpha),a)$ で定義する。
$\delta_s^*(\alpha)$ は状態 $s$ から始めて、文字列 $\alpha$ が入力された後の状態を表し、$\gamma_s^+(\alpha a)$ は状態 $s$ から始めて、文字列 $\alpha$ が入力された後の状態 $\delta_s^*(\alpha)$ で $a$ が入力された時の出力、すなわち文字列 $\alpha a$ が入力された後の出力を表す。すなわち $\transition{\;s_1\;}{a_1;b_1}\transition{\;s_2\;}{a_2;b_2}\cdots\labelarrow{a_{n-2};b_{n-2}}\transition{\;s_{n-1}\;}{a_{n-1};b_{n-1}}\transition{\;s_n\;}{a_n;b_n}$ のとき、$\delta_{s_1}^*(a_1a_2\cdots a_{n-1})=s_n,\ \gamma_{s_1}^+(a_1a_2\cdots a_{n-1}a_n)=b_n$である。このことを $\transition{\;s_1\;}{a_1a_2\cdots a_{n-1}}\transition{\;s_n\;}{a_n;b_n}$と表せば、 $\transition{\;s\;}{\alpha}\transition{\delta_s^*(\alpha)}{\beta}\transition{\delta_s^*(\alpha\beta)}{a;\gamma_s^+(\alpha\beta a)}$ なので、$\delta_s^*(\alpha\beta)=\delta_{\delta_s^*(\alpha)}^*(\beta),\ \gamma_s^+(\alpha\beta a)=\gamma^+_{\delta_s^*(\alpha)}(\beta a)$ が成立つ。
| 問.前頁の例のオートマトン $A$ に対し、以下の値を求めよ |
|
Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ において、入力列 $\alpha$ に対し、その最終出力を与える関数 $\gamma_{s_0}^+:\Sigma^+\to\Gamma$ を $A$ が実現(計算)する関数という。
$h:\Sigma^+ \to \Gamma,\ \alpha\in \Sigma^*$ に対し、$h_\alpha:\beta\in \Sigma^+ \mapsto h(\alpha\beta) \in \Gamma$ と定義する。特に $h_{\varepsilon}=h,\ (h_\alpha)_{\alpha'}=h_{\alpha\alpha'}$ である。
$h:\Sigma^+ \to \Gamma$ は、$\{h_\alpha \;|\; \alpha\in \Sigma^*\}$ が有限集合であるとき、正則関数であるいう。
| 問.$h:\Sigma^+ \to \Gamma,\ \alpha,\alpha'\in \Sigma^*,\ \beta\in\Sigma^+$ に対し、以下の式が成立つことを示せ |
|
定理.$h:\Sigma^+ \to \Gamma$ が正則である必要十分条件は、$h$ が Mealy オートマトンで実現されることである。
証明.$h:\Sigma^+ \to \Gamma$ に対し、Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ が存在して、$h=\gamma_{s_0}^+$ であるとする。$h_\alpha(\beta)=h(\alpha\beta)=\gamma^+_{s_0}(\alpha\beta)=\gamma_{\delta^*(s_0,\alpha)}^+(\beta)$ なので、$\{h_\alpha \;|\; \alpha\in \Sigma^*\}$ の要素数は、$A$ の状態数 $|S|$ を超えない。
逆に、$\{h_\alpha \;|\; \alpha\in \Sigma^*\}$ が有限ならば、Mealy オートマトン $A=(\{h_\alpha \;|\; \alpha\in \Sigma^*\},\Sigma,\Gamma,h,\delta,\gamma)$ を、$\delta(h_\alpha,x):=h_{\alpha x},\ \gamma(h_\alpha,x):=h(\alpha x)$ と定めれば、$\delta^*_{h_\alpha}(\beta):=h_{\alpha\beta}$ であるから、$\gamma_h^+(\alpha a)=\gamma(\delta^*_h(\alpha),a)=\gamma(h_\alpha,a)=h(\alpha a)$ より $h$ は $A$ で実現される。ここで定めたオートマトンは、$h$ を実現する状態数最小の Mealy オートマトンである。
□
次節以降の議論のために、定理を2つ証明しておこう。次の定理は、入力文字が共通の2つの Mealy オートマトンを並行的に動作させることができることを示している。
定理.$f:\Sigma^+\to \Gamma,\ g:\Sigma^+\to \Delta$ が正則ならば、$f\times g:\alpha\in \Sigma^+ \mapsto (f(\alpha),g(\alpha))\in \Gamma\times \Delta$ も正則である。
証明.Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma),\ B=(T,\Sigma,Z,t_0,\tau,\sigma)$ が存在して、$f(\alpha)=\gamma^+_{s_0}(\alpha),\ g(\alpha)=\sigma^+_{t_0}(\alpha)$ であるとする。それらの直積 $A\times B:=(S\times T,\Sigma,\Gamma\times Z,(s_0,t_0),\delta\times\tau,\gamma\times\sigma)$ を、 $\begin{cases} \delta\times\tau:((s,t),x)\in (S\times T)\times \Sigma \mapsto (\delta(s,x),\tau(t,x))\in S\times T \\ \gamma\times\sigma:((s,t),x)\in (S\times T)\times \Sigma \mapsto (\gamma(s,x),\sigma(t,x))\in \Gamma\times Z \end{cases}$
次の定理は、Mealy オートマトンの出力文字を置き換えてもよいことを示している。
定理.$f:\Sigma^+\to \Gamma,\ g:\Gamma\to \Delta$ で $f$ が正則ならば、$(g\circ f):\alpha\in \Sigma^+ \mapsto g(f(\alpha))\in \Delta$ も正則である。
証明.Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ が存在して、$f(\alpha)=\gamma_{s_0}^+(\alpha)$ であるとする。$A$ の出力文字 $a$ を $g(a)$ で書き変えたオートマトン $g\circ A :=(S,\Sigma,Z,s_0,\delta,g\circ\gamma)$ を、$g\circ\gamma:(s,x)\in S\times \Sigma \mapsto g(\gamma(s,x))\in \Delta$
定理.$f:\Sigma^+\to \Gamma,\ g:\Sigma^+\to \Delta$ が正則ならば、$f\times g:\alpha\in \Sigma^+ \mapsto (f(\alpha),g(\alpha))\in \Gamma\times \Delta$ も正則である。
証明.Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma),\ B=(T,\Sigma,Z,t_0,\tau,\sigma)$ が存在して、$f(\alpha)=\gamma^+_{s_0}(\alpha),\ g(\alpha)=\sigma^+_{t_0}(\alpha)$ であるとする。それらの直積 $A\times B:=(S\times T,\Sigma,\Gamma\times Z,(s_0,t_0),\delta\times\tau,\gamma\times\sigma)$ を、 $\begin{cases} \delta\times\tau:((s,t),x)\in (S\times T)\times \Sigma \mapsto (\delta(s,x),\tau(t,x))\in S\times T \\ \gamma\times\sigma:((s,t),x)\in (S\times T)\times \Sigma \mapsto (\gamma(s,x),\sigma(t,x))\in \Gamma\times Z \end{cases}$
で定義すれば、$A\times B$ は、$A,\ B$ の動作(状態遷移及び出力)を並行的に模倣するので、$f\times g(\alpha)=(\gamma\times\sigma)^+_{(s_0,t_0)}(\alpha)$ が成立ち、$f\times g$ を実現する。
□
次の定理は、Mealy オートマトンの出力文字を置き換えてもよいことを示している。
定理.$f:\Sigma^+\to \Gamma,\ g:\Gamma\to \Delta$ で $f$ が正則ならば、$(g\circ f):\alpha\in \Sigma^+ \mapsto g(f(\alpha))\in \Delta$ も正則である。
証明.Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ が存在して、$f(\alpha)=\gamma_{s_0}^+(\alpha)$ であるとする。$A$ の出力文字 $a$ を $g(a)$ で書き変えたオートマトン $g\circ A :=(S,\Sigma,Z,s_0,\delta,g\circ\gamma)$ を、$g\circ\gamma:(s,x)\in S\times \Sigma \mapsto g(\gamma(s,x))\in \Delta$
で定義すれば、$(g\circ f)(\alpha)=(g\circ\gamma)_{s_0}^+(\alpha)$ が成立つ。
□
| 問.$f,\,g:\Sigma^+\to \{0,1\}$が正則関数のとき次の関数も正則関数であることを示せ |
|
5.5節 有限オートマトン
本節およびこれに続く節の目的は、正則関数が正則言語と密接な関係があることを示す以下の目標を証明することである。目標.$L\subseteq \Sigma^*$ が正則 $\iff$ 正則関数 $f:\Sigma^+\to \Gamma$ と $c\in \Gamma$ が存在して $L-\{\varepsilon\}=f^{-1}(c)$
そのために、出力が $0,\ 1$ で次状態から定まる(制限された形の)Mealy オートマトンを考える。すなわち、$A=(S,\Sigma,\mathbb{B},s_0,\delta,\gamma)$ で、$o:S\to\mathbb{B}$ が存在して $\gamma(s,x)=o(\delta(s,x))$ と書けるものとする。このようなタイプのオートマトンを(決定性)有限オートマトンといい、$A:=(S,\Sigma,s_0,F,\delta)$ と表す。ここで、$S$ は状態の有限集合、$\Sigma$ は入力文字の有限集合、$s_0$ は開始状態、$F\ (=o^{-1}(1))\subseteq S$ は受理状態の集合、$\delta:S\times \Sigma\to S$ は状態遷移関数である。 受理状態を図示するときは2重丸$\dcircled{ }$で囲む。
| $\iff$ |
$\alpha\in \Sigma^*$ は $\delta_{\ s_0\ }^*(\alpha)\in F$、即ち${\Large\rhd}\transition{ }{\alpha}\dcircled{ }$($\alpha$ を読んだ後の状態が受理状態)のとき、$A$ で受理されるといい、$A$ が受理する文字列の集合 $L(A):=\{\alpha\;|\;\delta_{s_0}^*(\alpha)\in F\}=(\delta_{s_0}^*)^{-1}(F)=\{\alpha\;|\;{\Large\rhd}\transition{ }{\alpha}\dcircled{ }\}$ を $A$ が受理(認識)する言語という。有限オートマトンでは、開始状態が受理状態 $\left(s_0\in F,\ {\Large\rhd}\dcircled{ }\right)$ であることと空列が受理される($\varepsilon\in L(A)$)こととは同値である。
定理.$L\subseteq \Sigma^*$ が有限オートマトンで認識される$\iff$
正則関数 $f:\Sigma^+\to \Gamma$ と $c \in \Gamma$ が存在して $L-\{\varepsilon\}=f^{-1}(c)$
証明.$L$ が有限オートマトン $A=(S,\Sigma,s_0,F,\delta)$ で認識される($L=L(A)=\{\alpha\;|\;\delta_{s_0}^*(\alpha)\in F\}$ となる)とき、Mealy オートマトン $A'=(S,\Sigma,\mathbb{B},s_0,\delta,\gamma)$ を、$\gamma(s,x):=\begin{cases} 1 & \delta(s,x)\in F のとき\\ 0 & \delta(s,x)\not\in F のとき\end{cases}$ で定めれば、
$\alpha a \in L \iff A$ で $\delta^*_{s_0}(\alpha a)=\delta(\delta^*_{s_0}(\alpha),a)\in F$
$\iff A'$ で $\gamma^+_{s_0}(\alpha a)=\gamma(\delta^*_{s_0}(\alpha),a)=1 \iff \alpha a\in (\gamma_{s_0}^+)^{-1}(1)$。
よって、$A'$ が実現する正則関数 $\gamma_{s_0}^+$ により、$L-\{\varepsilon\}=(\gamma_{s_0}^+)^{-1}(1)$ と表せる。
逆に、Mealy オートマトン $A=(S,\Sigma,\Gamma,s_0,\delta,\gamma)$ が正則関数 $f=\gamma_{s_0}^+$ を実現しているとき、$c\in\Gamma$ に対し、有限オートマトンを $A'=(S\times \Gamma,\Sigma,(s_0,c),S\times\{c\},\tau)$、$\tau:((s,d),x)\mapsto (\delta(s,x),\gamma(s,x))$ と定めれば、状態に関する第一成分については、$\tau$ は $\delta$ と等しいから $\tau^*_{(s_0,c)}(\alpha)\in\{\delta^*_{s_0}(\alpha)\}\times\Gamma$ が成立つ。よって
$\alpha a\in f^{-1}(c)=(\gamma_{s_0}^+)^{-1}(c) \iff A$ で $\gamma_{s_0}^+(\alpha a)=\gamma(\delta_{s_0}^*(\alpha),a)=c$
$\iff A'$ で $\tau_{(s_0,c)}^*(\alpha a)=\tau(\tau_{(s_0,c)}^*(\alpha),a)=(\delta(\delta_{s_0}^*(\alpha),a),\gamma(\delta_{s_0}^*(\alpha),a))\in S\times\{c\} \iff \alpha a \in L(A')$。
したがって、我々の目標は次のように言い換えることができる。
目標.$L\subseteq \Sigma^*$ が正則 $\iff$ $L$ は有限オートマトンで認識できる
$\alpha a\in f^{-1}(c)=(\gamma_{s_0}^+)^{-1}(c) \iff A$ で $\gamma_{s_0}^+(\alpha a)=\gamma(\delta_{s_0}^*(\alpha),a)=c$
$\iff A'$ で $\tau_{(s_0,c)}^*(\alpha a)=\tau(\tau_{(s_0,c)}^*(\alpha),a)=(\delta(\delta_{s_0}^*(\alpha),a),\gamma(\delta_{s_0}^*(\alpha),a))\in S\times\{c\} \iff \alpha a \in L(A')$。
したがって、$f^{-1}(c)=(\gamma_{s_0}^+)^{-1}(c)=L(A')-\{\varepsilon\}$ であり、定理の直前に述べた事実より、$L-\{\varepsilon\}=L(A')-\{\varepsilon\}$ を満たす $L$ は(空列を含むか否かにかかわらず)有限オートマトンで認識される。
□
したがって、我々の目標は次のように言い換えることができる。
目標.$L\subseteq \Sigma^*$ が正則 $\iff$ $L$ は有限オートマトンで認識できる
5.6節 言語の方程式
「$L\subseteq \Sigma^*$ は有限オートマトンで認識できる $\Longrightarrow$ $L$ が正則」を示すために、言語の方程式を解くことを考える。定理.$\Sigma$上の言語の方程式 $X=LX\cup K,\ (L,K\subseteq\Sigma^*)$ に対し
- 包含関係における最小解は $X=L^*K$ である。
- $\varepsilon\not\in L$ ならば $X=L^*K$ が唯一の解である
2.$X=LX\cup K\supset L^*K$ とする。$X-L^*K$ の最短の語を $\alpha$ とすると、$\alpha\not\in K$ より $\alpha \in LX=\{\beta\alpha'\;|\; \beta\in L,\alpha'\in X\}$。$\varepsilon\not\in L$ より、$|\alpha|=|\beta|+|\alpha'|\gt|\alpha'|$ となり、矛盾。
□
定理.有限オートマトン $A=(S,\Sigma,s_0,F,\delta)$ と $s\in S$ に対し、$s$ を開始状態にした時 $A$ が受理する言語を $X_s:=\{\alpha\;|\;\delta^*(s,\alpha)\in F\}$ と定義する。
- $L(A)=X_{s_0}$
- $\displaystyle X_s=\bigcup_{a \in \Sigma} \{a\}X_{\delta(s,a)}\cup K_s,\ \left(K_s=\begin{cases}\{\varepsilon\}& s\in F のとき\\ \emptyset & s\not\in F のとき\end{cases} \right)$
- $X_s$ は正則言語である
2.$\varepsilon \in X_s \iff s \in F$、$a\alpha \in X_s \iff \alpha \in X_{\delta(s,a)}$ より明らか。
3.下の例からも分かるように、言語の連立方程式 2. の解は $\{a\}\ (a\in\Sigma)$ と $\{\varepsilon\},\ \emptyset$ から和、連接、閉包演算で得られるので、正則集合である。
□
系.$L\subseteq \Sigma^*$ は有限オートマトンで認識できる $\Longrightarrow$ $L$ は正則
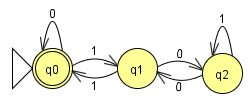
 例.右図の有限オートマトンが認識する言語を求めてみよう。言語の(連立)方程式は以下のようになる。以下、煩雑さを避けるために $\{,\}$ を省略した正則表現を用いる。
例.右図の有限オートマトンが認識する言語を求めてみよう。言語の(連立)方程式は以下のようになる。以下、煩雑さを避けるために $\{,\}$ を省略した正則表現を用いる。$\begin{cases} X_{q_0}=0X_{q_0}\cup 1X_{q_1}\cup \varepsilon & (1)\\ X_{q_1}=0X_{q_2}\cup 1X_{q_0} & (2)\\ X_{q_2}=0X_{q_1}\cup 1X_{q_2} & (3) \end{cases}$
(3) を解いて $X_{q_2}=1^*0X_{q_1}$。これを (2) に代入して解けば $X_{q_1}=01^*0X_{q_1}\cup 1X_{q_0}=(01^*0)^*1X_{q_0}$。これを (1) に代入して解けば $L(A)=X_{q_0}=0X_{q_0}\cup 1X_{q_1} \cup \varepsilon=(0\cup 1(01^*0)^*1)X_{q_0}\cup \varepsilon=(0\cup 1(01^*0)^*1)^*$ を得る。
5.7節 非決定性有限オートマトン
「$L\subseteq \Sigma^*$ が正則 $\Longrightarrow$ $L$ は決定性有限オートマトンで認識できる」を示すために、非決定性有限オートマトンを次のように定義する。これに対し、5.4節で定義した有限オートマトンを決定性有限オートマトンという。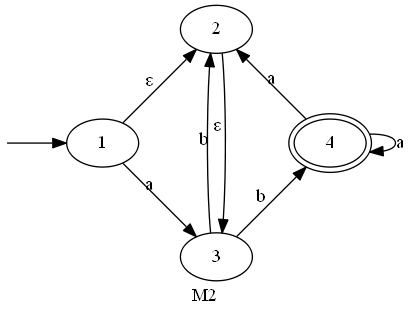
非決定性有限オートマトンは、$A:=(S,\Sigma,s_0,F,\Delta)$ で
- $S$ は状態の有限集合
- $\Sigma$ は入力文字の有限集合
- $s_0\in S$は開始状態
- $F\subseteq S$ は受理状態の集合
- $\Delta\subseteq S\times(\Sigma\cup\{\varepsilon\})\times S$ は状態遷移関係
非決定性有限オートマトン $A=(S,\Sigma,s_0,F,\Delta)$ に対し、$\Delta^*\subseteq S\times \Sigma^*\times S$ を以下のように帰納的に定義する。
- $(s,\varepsilon,s) \in \Delta^*$
- $(s,\alpha,t)\in\Delta^*,\ (t,a,u)\in \Delta \Longrightarrow (s,\alpha a,u)\Delta^*$
- 1. 2. で定義されものだけが $\Delta^*$ の要素である
さらに各状態 $s\in S$ に対し、 $\Delta_s^*:\alpha\in \Sigma^*\mapsto \{q\;|\;(s,\alpha,q)\in \Delta^*\}=\{q\;|\transition{s}{\alpha}\circled{q}\}\subseteq S$ と定義すれば、$\Delta_s^*(\alpha)$ は状態 $s$ から始めて、入力文字列 $\alpha$ で遷移可能な状態の集合を表す。
文字列 $\alpha\in \Sigma^*$ が非決定性有限オートマトン $A=(S,\Sigma,s_0,F,\Delta)$ で受理されるというのは、 $\Delta_{s_0}^*(\alpha)\cap F\ne\emptyset$ となる($\alpha$ で遷移可能な状態の中に受理状態がある)ときをいい、$A$ で受理される文字列の集合 $L(A):=\{\alpha\;|\;\Delta_{s_0}^*(\alpha)\cap F\ne\emptyset\}=(\Delta_{s_0}^*)^{-1}(\{Q\subseteq S\;|\;Q\cap F\ne\emptyset\})$ を $A$ が認識(受理)する言語という。
定理.任意の正則言語は非決定性有限オートマトンで認識される。
証明.正則言語の構成にそって、非決定性有限オートマトンの構成を示すことで証明する。
2つの非決定性有限オートマトン $A_i=(S_i,\Sigma,s_i,\{f_i\},\Delta_i),\ (i=1,2, S_1\cap S_2=\emptyset,\ s_0,f_0\not\in S_1\cup S_2)$ に対し、
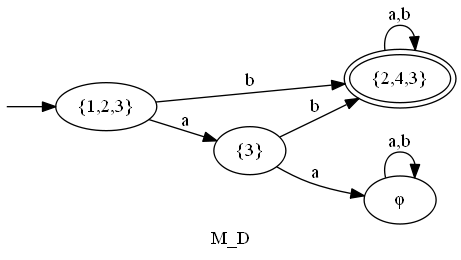
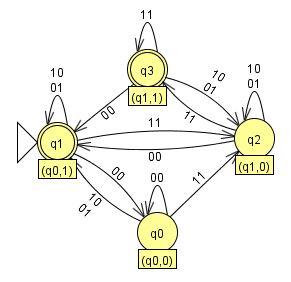
右図は前頁の非決定性有限オートマトンを決定性有限オートマトンに変換したものである。
これで、目標が達成できたので、定理として掲げておこう。
定理.$L\subseteq \Sigma^*$ が正則 $\iff$ $L$ は決定性有限オートマトンで認識できる
証明.正則言語の構成にそって、非決定性有限オートマトンの構成を示すことで証明する。
- $A_\emptyset:=(\{s_1,f_1\},\Sigma,s_1,\{f_1\},\emptyset)$ とおけば $L(A_\emptyset)=\emptyset$
- $a\in \Sigma\cup\{\varepsilon\}$ に対し $A_a:=(\{s_1,f_1\},\Sigma,s_1,\{f_1\},\{(s_1,a,f_1)\})$ とおけば $L(A_a)=\{a\}$
2つの非決定性有限オートマトン $A_i=(S_i,\Sigma,s_i,\{f_i\},\Delta_i),\ (i=1,2, S_1\cap S_2=\emptyset,\ s_0,f_0\not\in S_1\cup S_2)$ に対し、
- $A_1A_2:=(S_1\cup S_2,\Sigma,s_1,\{f_2\},\Delta_1\cup\{(f_1,\varepsilon,s_2)\}\cup\Delta_2)$ と定義すれば $L(A_1A_2)=L(A_1)L(A_2)$
- $A_1\cup A_2:=(S_1\cup S_2\cup\{s_0,f_0\},\Sigma,s_0,\{f_0\},\Delta_1\cup\Delta_2\cup\{(s_0,\varepsilon,s_1),(f_1,\varepsilon,f_0),(s_0,\varepsilon,s_2),(f_2,\varepsilon,f_0)\})$ と定義すれば $L(A_1\cup A_2)=L(A_1)\cup L(A_2)$
- $A_1^*:=(S_1\cup\{s_0,f_0\},\Sigma,s_0,\{f_0\},\Delta_1\cup\{(s_0,\varepsilon,f_0),(s_0,\varepsilon,s_1),(f_1,\varepsilon,s_1),(f_1,\varepsilon,f_0)\})$ と定義すれば $L(A_1^*)=L(A_1)^*$
であるから、$L_1,\ L_2$ が非決定性有限オートマトンで認識されれば、$L_1L_1,\ L_1\cup L_2,\ L_1^*$ も非決定性有限オートマトンで認識される。よって、正則言語は非決定性有限オートマトンで認識される。
□
決定性有限オートマトンへの変換
非決定性有限オートマトン $A=(S,\Sigma,s_0,F,\Delta)$ に対し、それと同じ言語を認識する 決定性有限オートマトンを $A':=(\{\Delta_{s_0}^*(\alpha)\;|\;\alpha\in\Sigma^*\},\Sigma,\Delta_{s_0}^*(\varepsilon),\{\Delta_{s_0}^*(\alpha)\;|\;\Delta_{s_0}^*(\alpha)\cap F\ne\emptyset\},\delta),\ \delta(\Delta_{s_0}^*(\alpha),x):=\Delta_{s_0}^*(\alpha x)$ と定義すれば、$\delta^*_{\Delta_{s_0}^*(\varepsilon)}(\alpha)=\Delta_{s_0}^*(\alpha)$ が成立つから、 $\alpha\in L(A)\iff \Delta_{s_0}^*(\alpha)\cap F\ne\emptyset \iff \delta^*_{\Delta_{s_0}^*(\varepsilon)}(\alpha)\in \{\Delta_{s_0}^*(\alpha)\;|\;\Delta_{s_0}^*(\alpha)\cap F\ne\emptyset\} \iff \alpha\in L(A')$ である。| 問. |
| $\delta^*_{\Delta_{s_0}^*(\varepsilon)}(\alpha)=\Delta_{s_0}^*(\alpha)$ を $\alpha$ に関する帰納法で証明せよ |

右図は前頁の非決定性有限オートマトンを決定性有限オートマトンに変換したものである。
これで、目標が達成できたので、定理として掲げておこう。
定理.$L\subseteq \Sigma^*$ が正則 $\iff$ $L$ は決定性有限オートマトンで認識できる
5.8節 正則言語の“正則”性
言語 $L\subseteq\Sigma^*$ と $\alpha\in\Sigma^*$ に対し、$L_\alpha=\{\beta\;|\;\alpha\beta\in L\}$ と定義すれば、正則関数と同様の定理が成立つ。定理.言語 $L\subseteq \Sigma^*$ 有限オートマトンで認識される$\iff |\{L_\alpha\;|\;\alpha\in\Sigma^*\}|\lt\infty$。
| 問. |
| 上の定理を証明せよ。 |
これまでの議論をまとめると
定理.言語 $L\subseteq \Sigma^*$ の関する次の条件はすべて同値である。
- 正則である
- 正則言語を係数に持つ連立右線形方程式の解である
- 非決定性有限オートマトンで認識される
- 決定性有限オートマトンで認識される
- $L-\{\varepsilon\}$ は正則関数の逆像である
- $|\{L_\alpha\;|\;\alpha\in\Sigma^*\}|\lt\infty$
定理.正則言語 $K,\ L$ に関し次が成立つ。
- $K\cup L,\ K\cap L,\ K-L,\ \Sigma^*-L$ も正則言語である。
- $L^R:=\{a_1a_2\cdots a_n\;|\;a_n\cdots a_2a_1\in L\}$ も正則言語である
| 問. |
| 上の定理を証明せよ |
5.9節 正規表現
正規(正則)表現は、一般のテキスト(文字列)に対して強力なパターンマッチング機能を提供する。正規表現はテキスト処理に威力を発揮するとともに、インターネット上でも正規表現による検索が可能なサービスが多数存在する。正規表現の記法
コンピュータ(システム)で使われる正規表現には、表現を簡潔にするために、様々な記法が工夫されている。それを紹介しよう。(1)基本演算:正規表現の基本演算は次の3種類の演算である。
| 記法 | 説明 | 使用例 |
| 連接 | 正規表現を続けて書けば、それらを続けた文字列と合致 | abc と def の連接は abcdef |
| | | 和(または)。どちらかのパターンと合致すれば合致。 | (this|that) is a sample → this is a sample、that is a sample と合致 |
| * | 直前の文字(文字列)の0回以上の繰り返しと合致 | 12* → 1、12、122、・・・ と合致。 (ab)*a →a、aba、ababa、・・・と合致。 |
正規表現では、基本演算の他に便利のために種々の演算・記法が用意される。
(2)繰り返し指定:直前の文字(列)の繰り返し回数を指定する
| 記法 | 説明 | 使用例 |
| + | 1回以上の繰り返し | 12+ → 12、122、・・・ と合致 12+=122* |
| ? | 0,1回の繰り返し | 12? → 1、12 と合致 12?=1|12 |
| {n} | n回繰り返し | (ab){3} → abababに合致 |
| {n, } | n回以上繰り返し | a{3,} →aaa、aaaa、…に合致 |
| {m,n} | m~n回繰り返し | a{3,5} →aaa、aaaa、aaaaaに合致 |
(3)文字の集合:1文字指定する
合致する文字列は、通常はパターンに適合する最長の文字列(最長合致)であるが、"?"を付加する事によって最短合致となる。
12+ →1222222222 に対し10桁目の1222222222までと合致
12+? →1222222222 に対し2桁目の12までと合致
(4)特殊な意味を持つ文字
その他特殊な意味を持つ文字
| 記法 | 説明 | 使用例 |
| . | 改行文字を除く任意の1文字 | windows.. windowsの後に2文字続く文字列と合致 |
| [ ] | [ ] 内に並べた文字のどれか | [ab]=a|b |
| - | 文字の区間。[ ] 内で用いる | [a-z]=a|b|・・・|z a-zの小文字アルファベット全て [0-9]=0|1|・・・|9 全角の数字 [0-9A-Z] 大文字のアルファベットか数字 |
| ^ | 否定。[ ] 内で用いる | [^a-z] 小文字のアルファベット以外全て |
合致する文字列は、通常はパターンに適合する最長の文字列(最長合致)であるが、"?"を付加する事によって最短合致となる。
12+ →1222222222 に対し10桁目の1222222222までと合致
12+? →1222222222 に対し2桁目の12までと合致
(4)特殊な意味を持つ文字
| 記法 | 説明 | 使用例 |
| ^ | 行頭 | ^abc →行頭にある abc と合致 |
| $ | 行末 | abc$ →行末にある abc と合致 |
|
|
正規表現による検索と置換
正規表現による検索を用いると、例えば英語の学習に役立つばかりでなく、文書・文献の特徴を数量的に抽出し、著者の異同や時代の推定、思想と文体との関係等を分析することも可能になる。その意味で、正規表現は文体の処理・解析のための重要なツールになっている。| 実習.正規表現検索を用いた英文分析 |
|
| 実習.正規表現による検索・置換 |
次ページは Java Script で実装した正規表現による検索・置換機能である。検索文字列や置換文字列を指定して[検索]、[置換]を押すと結果が下の欄に表示される。1.~4. を表す正規表現を求めよ。また、5.の置換を行え。
|
第6章 論理関数族の理論
関数の集合を関数族という。本章では、3.4節で2変数論理関数族について扱った、完全性および不完全性の問題を、より一般的に議論する。与えられた論理関数族 $\mathcal{F}$ が完全であることを示すには、$\mathcal{F}$ の関数を使って、完全であると知られている論理関数族、例えば $\{\cdot,\ +,\ ^-\}$ のすべての関数を合成してみせればよいが、完全でないことを示すには、より精密な議論が必要になる。6.1節 関数の合成の定義
$n$ 変数論理関数全体を $\mathcal{B}_n:=\{f\;|\; f:\mathbb{B}^n\to\mathbb{B}\}$、論理関数全体を $\displaystyle \mathcal{B}:=\bigcup_{n=0}^\infty \mathcal{B}_n$ 、恒等関数を $I:x\mapsto x$ で表す。論理関数 $f\in \mathcal{B}$ に 論理関数族 $\mathcal{G}\subseteq \mathcal{B}$ を合成して得られる関数の全体を
$f\otimes\mathcal{G}:=\{h:(x_1,\cdots,x_q)\mapsto f(g_1(x_{11},\cdots,x_{1n_1}),g_2(x_{21},\cdots,x_{2n_2}),\cdots,g_p(x_{p1},\cdots,x_{pn_p}))\;|\;$
$g_1,g_2,\cdots,g_p\in\mathcal{G}\cup\{I\},\ x_{11},\cdots,x_{1n_1},x_{21},\cdots,x_{2n_2},\cdots,x_{p1},\cdots,x_{pn_p}\in \{x_1,\cdots,x_q\}\}$
で定義する。即ち、$f\otimes\mathcal{G}$ に属し $x_1,\cdots,x_q$ を変数とする論理関数は、$f$ の各変数に、$x_1,\cdots,x_q$(の一部)を(重複を許して)変数に持つ $\mathcal{G}\cup\{I\}$ の関数を代入して得られる関数である。論理関数族 $\mathcal{F},\mathcal{G}\subseteq \mathcal{B}$ に対し、$\displaystyle \mathcal{F}\otimes\mathcal{G}:=\bigcup_{f\in\mathcal{F}}f\otimes\mathcal{G}$ と定義する。
|
{"width":260, "height":100, "showToolbox":false,
"toolbox":[{"type":"NOT"},{"type":"AND"},{"type":"OR"},{"type":"DC"},{"type":"LED"},{"type":"Toggle"}],
"devices":[
{"type":"DC","id":"dev0","x":0,"y":24,"label":"DC"},
{"type":"Toggle","id":"dev1","x":40,"y":0,"label":"x","state":{"on":false}},
{"type":"Toggle","id":"dev2","x":40,"y":48,"label":"y","state":{"on":false}},
{"type":"NOT","id":"dev3","x":88,"y":0,"label":"NOT"},
{"type":"NOT","id":"dev4","x":88,"y":48,"label":"NOT"},
{"type":"AND","id":"dev5","x":136,"y":0,"label":"AND"},
{"type":"AND","id":"dev6","x":136,"y":48,"label":"AND"},
{"type":"OR","id":"dev7","x":184,"y":24,"label":"OR"},
{"type":"LED","id":"dev8","x":232,"y":24,"label":"F(x,y)"}
],
"connectors":[
{"from":"dev1.in0","to":"dev0.out0"},
{"from":"dev2.in0","to":"dev0.out0"},
{"from":"dev3.in0","to":"dev1.out0"},
{"from":"dev4.in0","to":"dev2.out0"},
{"from":"dev5.in0","to":"dev3.out0"},
{"from":"dev5.in1","to":"dev2.out0"},
{"from":"dev6.in0","to":"dev1.out0"},
{"from":"dev6.in1","to":"dev4.out0"},
{"from":"dev7.in0","to":"dev5.out0"},
{"from":"dev7.in1","to":"dev6.out0"},
{"from":"dev8.in0","to":"dev7.out0"}
]
}
|
- 右図の回路に対応する表記は $+(\cdot(^-(x),I(y)),\cdot(^-(y),I(x)))$
- 関数の変数が右辺の定義式に現れなくともよい。例えば
$h(x,y,z)=f(g(y,x),x,y)=f(g(y,x),I(x),I(y))\in f\otimes\{g\}$
$\displaystyle \mathcal{F}^{(1)}:=\mathcal{F}\otimes\{I\}=\{h:(x_1,\cdots,x_q)\mapsto f(x_{11},\cdots,x_{p1})\;|\; f\in\mathcal{F},\ x_{11},\cdots,x_{p1}\in\{x_1,\cdots,x_q\}\},$
$\displaystyle \mathcal{F}^{(n)}:=\mathcal{F}^{(n-1)}\otimes\mathcal{F}^{(1)},\ \mathcal{F}^{(*)}:=\bigcup_{n=1}^\infty\mathcal{F}^{(n)}$ と定義する。
$\mathcal{F}^{(*)}$ を $\mathcal{F}$ の閉包といい、$h\in\mathcal{F}^{(*)}$ は $\mathcal{F}$ から合成されるという。
$\mathcal{F}=\mathcal{F}^{(*)}$ のとき、$\mathcal{F}$ は、閉関数族(クローン)である、(合成に関して)閉じている、という。
定理.$\mathcal{F}=\mathcal{F}^{(*)}\iff \mathcal{F}\otimes\mathcal{F}=\mathcal{F}$
定理.関数族 $\{\cdot,\ +,\ ^-\},\ \{\cdot,\ ^-\},\ \{+,\ ^-\},\ \{{\bf 1},\ \cdot,\ \oplus\},\ \{\,|\,\},\ \{\,\downarrow\,\}$ は完全である。
定理.
したがって、本章の目標は $\mathcal{B}$ の5個の極大関数族をすべて具体的に求めることである。
定理.$\mathcal{F}=\mathcal{F}^{(*)}\iff \mathcal{F}\otimes\mathcal{F}=\mathcal{F}$
完全の定義
$\mathcal{F}^{(*)}=\mathcal{B}$ のとき、$\mathcal{F}$ は完全であるという。3.4節の議論から次が言える。定理.関数族 $\{\cdot,\ +,\ ^-\},\ \{\cdot,\ ^-\},\ \{+,\ ^-\},\ \{{\bf 1},\ \cdot,\ \oplus\},\ \{\,|\,\},\ \{\,\downarrow\,\}$ は完全である。
極大の定義
閉論理関数族 $\mathcal{F}\subset \mathcal{B}$ が極大(関数族)であるというのは、$\mathcal{F}$ を真に含む閉関数族が $B$ のみであるときをいう。実は極大関数族は $5$ 個しかないことが知られている。それがすべて求まれば、次が言える。定理.
- 関数族 $\mathcal{F}$ が極大で $f\not\in \mathcal{F}$ ならば、$\mathcal{F}\cup \{f\}$ は完全である。
- 関数族 $\mathcal{F}$ が完全である必要十分条件は、$\mathcal{F}$ がどの極大関数族にも含まれないことである
- 完全関数族 $\mathcal{F}$ が極小(他の完全関数族を含まない)ならば、$|\mathcal{F}|\leqq 5$ である
| 問. |
| 直前の定理を証明せよ |
したがって、本章の目標は $\mathcal{B}$ の5個の極大関数族をすべて具体的に求めることである。
6.2節 閉関数族
| $0$ | $1$ | $2$ | $3$ | |
| $x$ | $\bf 0$ | $I$ | $\,^-$ | $\bf 1$ |
| $0$ | $0$ | $0$ | $1$ | $1$ |
| $1$ | $0$ | $1$ | $0$ | $1$ |
1変数関数に関する合成を考えると、次が言える。
- $\mathcal{F},\mathcal{G}\subseteq\mathcal{B}_1$ ならば
- $\mathcal{F}\otimes\mathcal{G}=\{h:(x_1,\cdots,x_n)\mapsto f(g(x_i))\;|\;f\in\mathcal{F},\ g\in\mathcal{G}\cup I\}$
- $(\mathcal{F}\otimes\mathcal{G})\cap\mathcal{B}_1=\{f(g(x))\;|\;f\in\mathcal{F},\ g\in\mathcal{G}\cup I\}$
- $\mathcal{F}\subseteq\mathcal{B},\ \mathcal{G}\subseteq\mathcal{B}_1$ ならば $(\mathcal{F}\otimes\mathcal{G})\cap\mathcal{B}_1 =\{f(g_1(x),\cdots,g_p(x))\;|\;f(x_1,\cdots,x_p)\in\mathcal{F},\ g_1(x),\cdots,g_p(x)\in\mathcal{G}_1\cup\{I\}\}$
- $\mathcal{F}\subseteq\mathcal{B}_1$ に対しては、 $\mathcal{F}^{(*)}\cap\mathcal{B}_1=\mathcal{F}\ \left(=\{f(g(x))\;|\;f\in\mathcal{F},g\in\mathcal{F}\cup I\}\right)$ のとき、$\mathcal{F}$ は閉じているという。
- $\mathcal{F} \subseteq \mathcal{B}_1$ が閉じていれば $\mathcal{F} \in$ $ \{\{I\},\ \{{\bf 0}\},\ \{{\bf 1}\},\ \{{\bf 0},{\bf 1}\},\ \{I,{\bf 0}\},\ \{I,{\bf 1}\},\ \{I,\,^-\},\ \{I,{\bf 0},{\bf 1}\},\ \mathcal{B}_1\}$
- $\mathcal{F}$が閉じていれば
- $\mathcal{F}\cap\mathcal{B}_1,\ (\mathcal{F}\cap\mathcal{B}_1)\cup\{I\}$ も閉じている
- $\mathcal{B}_1\not\subseteq\mathcal{F}\Rightarrow \mathcal{B}_1\not\subseteq\mathcal{F}\cup\{I\}$
| 問. |
| 上の 5.の a., b.を証明せよ |
したがって $I$ を含む $\mathcal{F}\subset\mathcal{B}$ が閉じていれば、$\mathcal{F}\cap\mathcal{B}_1$ も閉じていて、$\{I\}$、$\{I,{\bf 0}\}$、$\{I,{\bf 1}\}$、$\{I,\,^-\}$、$\{I,{\bf 0},{\bf 1}\}$、$\mathcal{B}_1$ のどれかになる。それぞれの場合について、$\mathcal{F}$ がどのような関数族になるかを調べるために、$I\in \mathcal{G}\subseteq\mathcal{B}_1$ に対し、$\mathcal{G}$ を保存する(多変数)論理関数の族を
$F(\mathcal{G}):=\{f\in\mathcal{B}\;|\;(f\otimes\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G}\}=\{f\;|\;g_1(x),\cdots,g_p(x)\in \mathcal{G} \Rightarrow f(g_1(x),\cdots,g_p(x))\in \mathcal{G} \}$
と定義する。
後で示すが、$B_1$ を包含しない極大閉関数族はすべて $F(\mathcal{G})$ の形に書け、$F(\mathcal{G})\cap\mathcal{B}_1=\mathcal{G}$ である。まず $F(\mathcal{G})$ がどのような関数族になるか調べよう。- $F(\{I\})=\{f\;|\;f(x,\cdots,x)=x\}$ 等値保存関数族
- $\because)\ f\in F(\{I\})\Leftrightarrow f(I(x),\cdots,I(x))=I(x)$
- $F(\{I,{\bf 0}\})=\{f\;|\;f(0,\cdots,0)=0\}$ $0$値保存関数族
- $\because)\ g\in \{I,{\bf 0}\}\Leftrightarrow g(0)=0$より
$"g_1,\cdots,g_p\in\{I,{\bf 0}\}$に対し $h(x):=f(g_1(x),\cdots,g_p(x))\in\{I,{\bf 0}\}"\iff h(0)=f(0,\cdots,0)=0$ - $F(\{I,{\bf 1}\})=\{f\;|\;f(1,\cdots,1)=1\}$ $1$値保存関数族
- $\because)\ g\in \{I,{\bf 1}\}\Leftrightarrow g(1)=1$より
$"g_1,\cdots,g_p\in\{I,{\bf 1}\}$に対し $h(x):=f(g_1(x),\cdots,g_p(x))\in\{I,{\bf 1}\}"\iff h(1)=f(1,\cdots,1)=1$
- $F(\{I,\,^-\})=\{f\;|\;\bar{f(x_1,\cdots,x_n)}=f(\bar{x_1},\cdots,\bar{x_n})\}$ 自己双対関数族
- $\because)\ g\in \{I,\,^-\}\Leftrightarrow g(0)\ne g(1)\Leftrightarrow \bar{g(x)}=g(\bar{x})$より
$"g_1,\cdots,g_p\in\{I,\,^-\}$に対し $h(x):=f(g_1(x),\cdots,g_p(x))\in\{I,\,^-\}$
$\Leftrightarrow \bar{h(x)}=\bar{f(g_1(x),\cdots,g_p(x))}=h(\bar{x})=f(g_1(\bar{x}),\cdots,g_p(\bar{x}))=f(\bar{g_1(x)},\cdots,\bar{g_p(x)})"$
$\iff \bar{f(x_1,\cdots,x_p)}=f(\bar{x_1},\cdots,\bar{x_p})$ - $F(\{I,{\bf 0},{\bf 1}\})=\{f\;|\;x_1\leqq y_1,\cdots,x_n\leqq y_n \Rightarrow f(x_1,\cdots,x_n)\leqq f(y_1,\cdots,y_n)\}$ 単調増大関数族
- $\because)\ g\in \{I,{\bf 0},{\bf 1}\}\Leftrightarrow g(0)\leqq g(1)$より
$"g_1,\cdots,g_p\in\{I,{\bf 0},{\bf 1}\}$に対し $h(x):=f(g_1(x),\cdots,g_p(x))\in\{I,{\bf 0},{\bf 1}\}$
$\Leftrightarrow h(0)=f(g_1(0),\cdots,g_p(0))\leqq h(1)=f(g_1(1),\cdots,g_p(1)))"$
$\iff "x_1\leqq y_1,\cdots,x_n\leqq y_n \Rightarrow f(x_1,\cdots,x_n)\leqq f(y_1,\cdots,y_n)"$ - $F(\mathcal{B}_1)=\mathcal{B}$
- $\because)\ $明らか
| 問.次を求めよ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 問.次を示せ |
|
定理.$I\in \mathcal{G}=\mathcal{G}^{(*)} \subset \mathcal{B}_1$ ならば $F(\mathcal{G})\cap\mathcal{B}_1=\mathcal{G}$ かつ $\mathcal{B}_1 \not\subseteq F(\mathcal{G})=F(\mathcal{G})^{(*)}$
証明.3つに分けて証明する
($\mathcal{G}=\mathcal{G}^{(*)}\subset\mathcal{B}_1 \Longrightarrow\mathcal{G}\subseteq F(\mathcal{G})\cap\mathcal{B}_1$ の証明)定義より明らか
($I\in \mathcal{G} \subset \mathcal{B}_1\Longrightarrow F(\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G},\ \mathcal{B}_1 \not\subseteq F(\mathcal{G})$ の証明)$I\in \mathcal{G}$ と定義 $F(\mathcal{G}):=\{f\in\mathcal{B}\;|\;(f\otimes\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G}\}$ より、$f\in\mathcal{B}_1\cap F(\mathcal{G})\Rightarrow f\in f\otimes\mathcal{G}\cap\mathcal{B}_1\subseteq\mathcal{G}$。よって、$\mathcal{G}\subseteq F(\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G}\subset\mathcal{B}_1$。すなわち、 $\mathcal{B}_1 \not\subseteq F(\mathcal{G})$。
($I\in \mathcal{G} \subset \mathcal{B}_1\Longrightarrow F(\mathcal{G})=F(\mathcal{G})^{(*)}$ の証明)$F(\mathcal{G})\otimes F(\mathcal{G})\subseteq F(\mathcal{G})$ を示せばよい。$F(\mathcal{G})$ の定義から $I\in F(\mathcal{G})$。$h\in F(\mathcal{G})\otimes F(\mathcal{G})$ ならば、 関数 $f\in F(\mathcal{G})\cap\mathcal{B}_p$ と $g_1,g_2,\cdots,g_p\in F(\mathcal{G})\cup\{I\}=F(\mathcal{G})$、 $\{x_{11},\cdots,x_{1n_1},x_{21},\cdots,x_{2n_2},\cdots,x_{p1},\cdots,x_{pn_p}\}\subseteq\{x_1,\cdots,x_q\}$ が存在して、 $h(x_1,x_2,\cdots,x_q)=f(g_1(x_{11},\cdots,x_{1n_1}),g_2(x_{21},\cdots,x_{2n_2}),\cdots,g_p(x_{p1},\cdots,x_{pn_p}))$ と書ける。ここで、$h_1,h_2,\cdots,h_q\in \mathcal{G}$ に対し、$x_{ij}=x_k\Leftrightarrow h_{ij}=h_k$ とおけば $h(h_1(x),h_2(x),\cdots,h_q(x))=$
$f(g_1(h_{11}(x),\cdots,h_{1n_1}(x)),g_2(h_{21}(x),\cdots,h_{2n_2}(x)),\cdots,g_p(h_{p1}(x),\cdots,h_{pn_p}(x)))$ と書ける。よって、$g_i(h_{i1}(x),\cdots,g_{in_i}(x))\in \mathcal{G}$($i=1,\cdots,p$)と $f\in F(\mathcal{G})$ より、$h(h_1(x),h_2(x),\cdots,h_q(x))\in\mathcal{G}$ 即ち $h\in F(\mathcal{G})$ が言える。
定理.$\mathcal{B}_1 \not\subseteq \mathcal{F}=\mathcal{F}^{(*)} \Longrightarrow I \in \exists \mathcal{G}=\mathcal{G}^{(*)} \subset \mathcal{B}_1,\ \mathcal{F} \subseteq F(\mathcal{G})$
証明.$\mathcal{F}$ は閉じているので、$\mathcal{G}:=(\mathcal{F}\cap\mathcal{B}_1)\cup\{I\}$ も閉じている。$\mathcal{B}_1\not\subseteq \mathcal{F}$ より、$\mathcal{G}\subset\mathcal{B}_1$。
$f\in\mathcal{F}$ ならば、$(f\otimes\mathcal{G})\cap\mathcal{B}_1=(f\otimes((\mathcal{F}\cap\mathcal{B}_1)\cup\{I\}))\cap\mathcal{B}_1\subseteq (f\otimes \mathcal{F})\cap\mathcal{B}_1\subseteq \mathcal{F}\cap\mathcal{B}_1\subseteq \mathcal{G}$ より、$f\in F(\mathcal{G})$。
証明.3つに分けて証明する
($\mathcal{G}=\mathcal{G}^{(*)}\subset\mathcal{B}_1 \Longrightarrow\mathcal{G}\subseteq F(\mathcal{G})\cap\mathcal{B}_1$ の証明)定義より明らか
($I\in \mathcal{G} \subset \mathcal{B}_1\Longrightarrow F(\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G},\ \mathcal{B}_1 \not\subseteq F(\mathcal{G})$ の証明)$I\in \mathcal{G}$ と定義 $F(\mathcal{G}):=\{f\in\mathcal{B}\;|\;(f\otimes\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G}\}$ より、$f\in\mathcal{B}_1\cap F(\mathcal{G})\Rightarrow f\in f\otimes\mathcal{G}\cap\mathcal{B}_1\subseteq\mathcal{G}$。よって、$\mathcal{G}\subseteq F(\mathcal{G})\cap\mathcal{B}_1\subseteq\mathcal{G}\subset\mathcal{B}_1$。すなわち、 $\mathcal{B}_1 \not\subseteq F(\mathcal{G})$。
($I\in \mathcal{G} \subset \mathcal{B}_1\Longrightarrow F(\mathcal{G})=F(\mathcal{G})^{(*)}$ の証明)$F(\mathcal{G})\otimes F(\mathcal{G})\subseteq F(\mathcal{G})$ を示せばよい。$F(\mathcal{G})$ の定義から $I\in F(\mathcal{G})$。$h\in F(\mathcal{G})\otimes F(\mathcal{G})$ ならば、 関数 $f\in F(\mathcal{G})\cap\mathcal{B}_p$ と $g_1,g_2,\cdots,g_p\in F(\mathcal{G})\cup\{I\}=F(\mathcal{G})$、 $\{x_{11},\cdots,x_{1n_1},x_{21},\cdots,x_{2n_2},\cdots,x_{p1},\cdots,x_{pn_p}\}\subseteq\{x_1,\cdots,x_q\}$ が存在して、 $h(x_1,x_2,\cdots,x_q)=f(g_1(x_{11},\cdots,x_{1n_1}),g_2(x_{21},\cdots,x_{2n_2}),\cdots,g_p(x_{p1},\cdots,x_{pn_p}))$ と書ける。ここで、$h_1,h_2,\cdots,h_q\in \mathcal{G}$ に対し、$x_{ij}=x_k\Leftrightarrow h_{ij}=h_k$ とおけば $h(h_1(x),h_2(x),\cdots,h_q(x))=$
$f(g_1(h_{11}(x),\cdots,h_{1n_1}(x)),g_2(h_{21}(x),\cdots,h_{2n_2}(x)),\cdots,g_p(h_{p1}(x),\cdots,h_{pn_p}(x)))$ と書ける。よって、$g_i(h_{i1}(x),\cdots,g_{in_i}(x))\in \mathcal{G}$($i=1,\cdots,p$)と $f\in F(\mathcal{G})$ より、$h(h_1(x),h_2(x),\cdots,h_q(x))\in\mathcal{G}$ 即ち $h\in F(\mathcal{G})$ が言える。
定理.$\mathcal{B}_1 \not\subseteq \mathcal{F}=\mathcal{F}^{(*)} \Longrightarrow I \in \exists \mathcal{G}=\mathcal{G}^{(*)} \subset \mathcal{B}_1,\ \mathcal{F} \subseteq F(\mathcal{G})$
証明.$\mathcal{F}$ は閉じているので、$\mathcal{G}:=(\mathcal{F}\cap\mathcal{B}_1)\cup\{I\}$ も閉じている。$\mathcal{B}_1\not\subseteq \mathcal{F}$ より、$\mathcal{G}\subset\mathcal{B}_1$。
$f\in\mathcal{F}$ ならば、$(f\otimes\mathcal{G})\cap\mathcal{B}_1=(f\otimes((\mathcal{F}\cap\mathcal{B}_1)\cup\{I\}))\cap\mathcal{B}_1\subseteq (f\otimes \mathcal{F})\cap\mathcal{B}_1\subseteq \mathcal{F}\cap\mathcal{B}_1\subseteq \mathcal{G}$ より、$f\in F(\mathcal{G})$。
$\mathcal{B}_1$ を包含しない極大閉関数族はわかったので、$\mathcal{B}_1$ を含む閉関数族がどうなっているか調べよう。線型関数族を $\mathcal{L}:=\{f\;|\;f(x_1,\cdots,x_n)=a\oplus a_1x_1\oplus\cdots\oplus a_nx_n\}$ と定義する。
定理.$\mathcal{B}_1\subseteq \mathcal{F}=\mathcal{F}^{(*)} \Longrightarrow \mathcal{F}\in\{\mathcal{B}_1^{(*)},\ \mathcal{L},\ \mathcal{B}\}$
証明.明らかに、$\mathcal{B}_1^{(*)},\ \mathcal{L},\ \mathcal{B}$ は定理の仮定をみたし、その中で、$\mathcal{B}_1^{(*)}=\{f:(x_1,\cdots,x_n)\mapsto g(x_i)\;|\;g\in\mathcal{B}_1\}$ が最小で $\mathcal{B}$ が最大である。定理の仮定をみたす閉関数族が他にないことを示そう。
$\mathcal{B}_1^{(*)}\subset \mathcal{F}=\mathcal{F}^{(*)}\subseteq\mathcal{L}$とする。$a$ や $a\oplus x$ で表される関数は本質的 $1$ 又は $0$ 変数関数で $\mathcal{B}_1^{(*)}$ に含まれるので、$f(x_1,\cdots,x_p)=a\oplus a_1x_1\oplus\cdots\oplus a_px_p \in \mathcal{F}$ で少なくとも2つの $a_i$ が $0$ でないものが存在する。今 $a_1=a_2=1$ であるとすると、 $g(x_1,x_2)=f(x_1,x_2,0,\cdots,0)=a\oplus x_1\oplus x_2 \in\mathcal{F}$ である。$a=0,1$ にかかわらず $a\oplus x \in \{I,\ ^-\}\subseteq\mathcal{B}_1$ なので、$\mathcal{F}\supseteq(\mathcal{B}_1\cup \{g(x_1,x_2)=a\oplus x_1\oplus x_2\})^{(*)}=(\mathcal{B}_1\cup \{x_1\oplus x_2\})^{(*)}=\mathcal{L}=\mathcal{F}$。
$\mathcal{B}_1^{(*)}\subset \mathcal{F}=\mathcal{F}^{(*)}\not\subseteq\mathcal{L}$とする。 $f\in \mathcal{F}-\mathcal{L}$ のガロア標準形 $\displaystyle f(x_1,x_2,\cdots,x_n)=\bigoplus_{A\subseteq\{1,2,\cdots,n\}}\left(a_A\prod_{i\in A}x_i\right)$ の2次以上の項の中に係数が $0$ でないものが存在する。今その中で最低次の項を $x_1x_2\cdots x_k$ とし、$x_3,\cdots,x_k$ に $1$ を、$x_{k+1},\cdots,x_n$ に $0$ を、代入すれば、$g(x_1,x_2):=f(x_1,x_2,1,\cdots,1,0,\cdots,0)=a_\emptyset\oplus a_{\{1\}}x_1\oplus a_{\{2\}}x_2\oplus x_1x_2\in\mathcal{F}$。さらに $a\oplus x \in \mathcal{B}_1\subseteq \mathcal{F}$ より、$h(x_1,x_2):=g(a_{\{2\}}\oplus x_1,a_{\{1\}}\oplus x_2)=a_\emptyset\oplus a_{\{1\}}(a_{\{2\}}\oplus x_1)\oplus a_{\{2\}}(a_{\{1\}}\oplus x_2)\oplus(a_{\{2\}}\oplus x_1)(a_{\{1\}}\oplus x_2)$
$=(a_\emptyset\oplus a_{\{1\}}a_{\{2\}})\oplus x_1x_2\in\mathcal{F}$。
$a_\emptyset\oplus a_{\{1\}}a_{\{2\}}=1$ ならば $h(x_1,x_2)=x_1|x_2$ なので $\mathcal{F}\supseteq\{|\}^{(*)}=\mathcal{B}=\mathcal{F}$、 $a_\emptyset\oplus a_{\{1\}}a_{\{2\}}=0$ ならば $h(x_1,x_2)=x_1\cdot x_2$ なので $\mathcal{F}\supseteq\{\cdot,\ ^-\}^{(*)}=\mathcal{B}=\mathcal{F}$。よって証明された。
定理.極大閉関数族は、$F(\{I,{\bf 0}\}),\ F(\{I,{\bf 1}\}),\ F(\{I,\,^-\}),\ F(\{I,{\bf 0},{\bf 1}\}),\ \mathcal{L}$ の5個である。
証明. $I\in \mathcal{G}=\mathcal{G}^{(*)} \subset \mathcal{B}_1$ をみたす $\mathcal{G}$ は $\{I\},\ \{I,{\bf 0}\},\ \{I,{\bf 1}\},\ \{I,\,^-\},\ \{I,{\bf 0},{\bf 1}\}$ の5個で、$F(\{I\})$ は極大ではないから、$\mathcal{B}_1\not\subseteq \mathcal{F}$ を満たす極大閉関数族は $F(\{I,{\bf 0}\}),\ F(\{I,{\bf 1}\}),\ F(\{I,\,^-\}),\ F(\{I,{\bf 0},{\bf 1}\})$ の4つ(前頁の問)。前定理より、$\mathcal{B}_1 \subseteq \mathcal{F}$ を満たす極大閉関数族は $\mathcal{L}$ のみである。
これで本章の目標が達成された。
定理.$\mathcal{B}_1\subseteq \mathcal{F}=\mathcal{F}^{(*)} \Longrightarrow \mathcal{F}\in\{\mathcal{B}_1^{(*)},\ \mathcal{L},\ \mathcal{B}\}$
証明.明らかに、$\mathcal{B}_1^{(*)},\ \mathcal{L},\ \mathcal{B}$ は定理の仮定をみたし、その中で、$\mathcal{B}_1^{(*)}=\{f:(x_1,\cdots,x_n)\mapsto g(x_i)\;|\;g\in\mathcal{B}_1\}$ が最小で $\mathcal{B}$ が最大である。定理の仮定をみたす閉関数族が他にないことを示そう。
$\mathcal{B}_1^{(*)}\subset \mathcal{F}=\mathcal{F}^{(*)}\subseteq\mathcal{L}$とする。$a$ や $a\oplus x$ で表される関数は本質的 $1$ 又は $0$ 変数関数で $\mathcal{B}_1^{(*)}$ に含まれるので、$f(x_1,\cdots,x_p)=a\oplus a_1x_1\oplus\cdots\oplus a_px_p \in \mathcal{F}$ で少なくとも2つの $a_i$ が $0$ でないものが存在する。今 $a_1=a_2=1$ であるとすると、 $g(x_1,x_2)=f(x_1,x_2,0,\cdots,0)=a\oplus x_1\oplus x_2 \in\mathcal{F}$ である。$a=0,1$ にかかわらず $a\oplus x \in \{I,\ ^-\}\subseteq\mathcal{B}_1$ なので、$\mathcal{F}\supseteq(\mathcal{B}_1\cup \{g(x_1,x_2)=a\oplus x_1\oplus x_2\})^{(*)}=(\mathcal{B}_1\cup \{x_1\oplus x_2\})^{(*)}=\mathcal{L}=\mathcal{F}$。
$\mathcal{B}_1^{(*)}\subset \mathcal{F}=\mathcal{F}^{(*)}\not\subseteq\mathcal{L}$とする。 $f\in \mathcal{F}-\mathcal{L}$ のガロア標準形 $\displaystyle f(x_1,x_2,\cdots,x_n)=\bigoplus_{A\subseteq\{1,2,\cdots,n\}}\left(a_A\prod_{i\in A}x_i\right)$ の2次以上の項の中に係数が $0$ でないものが存在する。今その中で最低次の項を $x_1x_2\cdots x_k$ とし、$x_3,\cdots,x_k$ に $1$ を、$x_{k+1},\cdots,x_n$ に $0$ を、代入すれば、$g(x_1,x_2):=f(x_1,x_2,1,\cdots,1,0,\cdots,0)=a_\emptyset\oplus a_{\{1\}}x_1\oplus a_{\{2\}}x_2\oplus x_1x_2\in\mathcal{F}$。さらに $a\oplus x \in \mathcal{B}_1\subseteq \mathcal{F}$ より、$h(x_1,x_2):=g(a_{\{2\}}\oplus x_1,a_{\{1\}}\oplus x_2)=a_\emptyset\oplus a_{\{1\}}(a_{\{2\}}\oplus x_1)\oplus a_{\{2\}}(a_{\{1\}}\oplus x_2)\oplus(a_{\{2\}}\oplus x_1)(a_{\{1\}}\oplus x_2)$
$=(a_\emptyset\oplus a_{\{1\}}a_{\{2\}})\oplus x_1x_2\in\mathcal{F}$。
$a_\emptyset\oplus a_{\{1\}}a_{\{2\}}=1$ ならば $h(x_1,x_2)=x_1|x_2$ なので $\mathcal{F}\supseteq\{|\}^{(*)}=\mathcal{B}=\mathcal{F}$、 $a_\emptyset\oplus a_{\{1\}}a_{\{2\}}=0$ ならば $h(x_1,x_2)=x_1\cdot x_2$ なので $\mathcal{F}\supseteq\{\cdot,\ ^-\}^{(*)}=\mathcal{B}=\mathcal{F}$。よって証明された。
| 問. |
|
定理.極大閉関数族は、$F(\{I,{\bf 0}\}),\ F(\{I,{\bf 1}\}),\ F(\{I,\,^-\}),\ F(\{I,{\bf 0},{\bf 1}\}),\ \mathcal{L}$ の5個である。
証明. $I\in \mathcal{G}=\mathcal{G}^{(*)} \subset \mathcal{B}_1$ をみたす $\mathcal{G}$ は $\{I\},\ \{I,{\bf 0}\},\ \{I,{\bf 1}\},\ \{I,\,^-\},\ \{I,{\bf 0},{\bf 1}\}$ の5個で、$F(\{I\})$ は極大ではないから、$\mathcal{B}_1\not\subseteq \mathcal{F}$ を満たす極大閉関数族は $F(\{I,{\bf 0}\}),\ F(\{I,{\bf 1}\}),\ F(\{I,\,^-\}),\ F(\{I,{\bf 0},{\bf 1}\})$ の4つ(前頁の問)。前定理より、$\mathcal{B}_1 \subseteq \mathcal{F}$ を満たす極大閉関数族は $\mathcal{L}$ のみである。
これで本章の目標が達成された。