集合と論理
・集合や論理の基本的な記号と概念について学びます。
・無限集合の奇妙な性質を学びます。
・集合や論理の素朴な理解から、矛盾が生じることを学びます。
1.集合とその記述
「もの」とその「表現」を区別しよう。
集合とは「もの」の集まりで、
(1) 表現が(表す「もの」が)等しいか否かの基準が明確
(2) 「もの」が集合に属するか否かの基準が明確
であるものを言う。
3種の「である」
(1) ポチは犬である:ポチ$\in$犬
(2) 犬は動物である:犬$\subseteq$動物
(3) 明けの明星は金星である:明けの明星$=$金星
パズル:次の議論は正しいか?
明けの明星は金星である(と等しい)。
宵の明星は金星である(と等しい)。
よって、明けの明星は宵の明星である(と等しい)。
2.外延的表記、内包的表記
集合の表記法には2種類ある。外延的表記:集合に属す要素(の表現)を{}内に列挙する
$\{$月、火、水、木、金、土、日$\}$、$\{1,2,3,\cdots\}$
要素の重複や、並び順は意味を持たない
$\{a,b,c,d,c,b\}=\{a,b,c,d\}=\{a,d,b,c\}$
内包的表記:ものが集合に属す(必要十分)条件を記述する
$\{x|x$は週の曜日である$\},\ \ \{x|x$は正整数である$\}$
内包的表記 $A=\{x|P_A(x)\}$では $x\in A \iff P_A(x)$
集合 $A$ と1変数の述語 $P_A(x)$を同一視。
ここで、1変数の述語は、ものに関する「属性」や「条件」
例えば、「犬」の集合は「犬である」ものの集合。
3.集合演算と論理演算
| 集合演算 | $X$ | $P_X(x)$ | 論理演算 |
| 共通部分 | $A\cap B$ | $P_A(x)\wedge P_B(x)$ | 論理積(かつ) |
| 和集合 | $A\cup B$ | $P_A(x)\vee P_B(x)$ | 論理和(または) |
| 補集合 | $A^c\ \ (=U-A)$ | $\neg P_A(x)$ | 否定(でない) |
| 差集合 | $A-B$ | $P_A(x) \wedge \neg P_B(x)$ | |
| ―― | $A^c \cup B$ | $P_A(x)\to P_B(x)$ | 含意(ならば) |
考えている世界(全体集合) $U$ を定めないと議論できない
集合は全体集合の部分集合
② $\{x|P_A(x)\to P_B(x)\}$の補集合($P_A(x)\to P_B(x)$の反例集合)は $A-B$
包含関係 ($\forall x$ は「すべての$x$に対して」)
$A\subseteq B \iff U=A^c\cup B \iff \forall x P_A(x)\to P_B(x)$
パズル.ベン図を使って $A\subseteq B \iff U=A^c\cup B$ を示せ。
4.空集合、全体集合、恒偽、恒真
| 集合 | 論理 | ||
| 空集合 | $\emptyset$ | $P_\emptyset(x)=F$ | 恒偽述語 |
| 全体集合 | $U$ | $P_U(x)=T$ | 恒真述語 |
| 集合の約束 | 論理の約束 | |
| $\emptyset\subseteq A$ | $\iff$ | $\forall x F\to P_A(x)$ |
| 空集合は任意の 集合の部分集合 | 偽の仮定からは何を 結論付けても正しい |
日常話法との乖離
通常「$P_A$ならば$P_B$」($P_A\to P_B$)は、前件$P_A$と後件$P_B$の間に何らかの論理的時間的因果関係が成り立つ場合に限られ、かつ前件をみたす要素が少なくとも一つあることが多い。
アリストテレスの名辞論理(1変数述語論理)では、名辞(が表す集合)は空集合ではない。
パズル:「叱れらないならば勉強しない」の対偶は「勉強するならば叱られる」である。これは正しいか。
6.ベン図と真理値表
| 領域 | 集合演算 | 1変数述語 | $P_A$ | $P_B$ | $P_C$ |
| 0 | $A^c\cap B^c\cap C^c$ | $\neg P_A(x)\wedge \neg P_B(x)\wedge \neg P_C(x)$ | 0 | 0 | 0 |
| 1 | $A^c\cap B^c\cap C$ | $\neg P_A(x)\wedge \neg P_B(x)\wedge P_C(x)$ | 0 | 0 | 1 |
| 2 | $A^c\cap B\cap C^c$ | $\neg P_A(x)\wedge P_B(x)\wedge \neg P_C(x)$ | 0 | 1 | 0 |
| 3 | $A^c\cap B\cap C$ | $\neg P_A(x)\wedge P_B(x)\wedge P_C(x)$ | 0 | 1 | 1 |
| 4 | $A\cap B^c\cap C^c$ | $P_A(x)\wedge \neg P_B(x)\wedge \neg P_C(x)$ | 1 | 0 | 0 |
| 5 | $A\cap B^c\cap C$ | $P_A(x)\wedge \neg P_B(x)\wedge P_C(x)$ | 1 | 0 | 1 |
| 6 | $A\cap B\cap C^c$ | $P_A(x)\wedge P_B(x)\wedge \neg P_C(x)$ | 1 | 1 | 0 |
| 7 | $A\cap B\cap C$ | $P_A(x)\wedge P_B(x)\wedge P_C(x)$ | 1 | 1 | 1 |
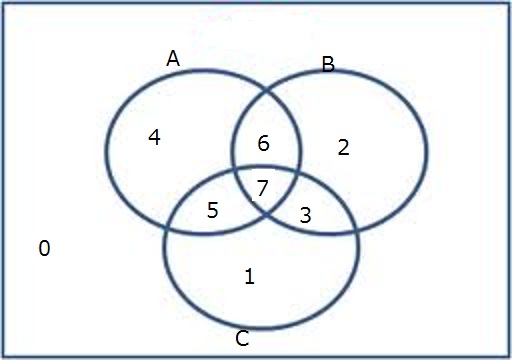
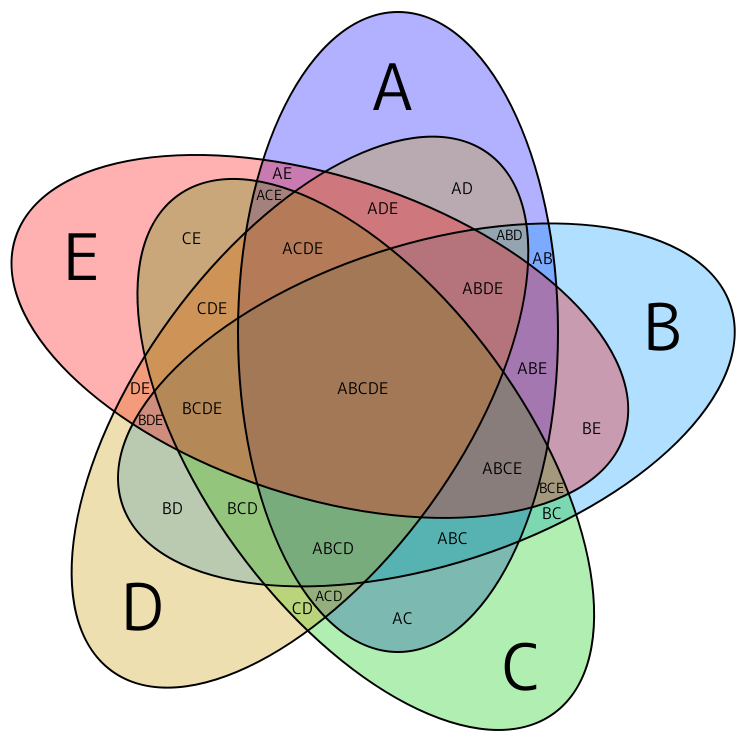
集合(1変数述語)で記述できる領域はすべて、
$\cap,\ \cup,\ {}^c$($\wedge,\ \vee,\ \neg$)の組合せで表せる。
7.ベキ集合とパラドックス
集合$A$に対し、$2^A:=\{x|x\subseteq A\}$を$A$のベキ集合という。$2^A$は、$A$の部分集合すべてからなる集合:$x\in 2^A\iff x\subseteq A$
例.$2^{\{a,b,c\}}=\{\emptyset,\{a\},\{b\},\{c\},\{a,b\},\{b,c\},\{c,a\},\{a,b,c\}\}$
パズル.$A$の要素数$|A|=n$のとき、$|2^A|$を求めよ。
ラッセルのパラドックス
集合を規定する1変数述語はどんなものでも許されるのか$M=\{x|x\not\in x\}$「自分自身を要素として含まない集合」の集合
$M$を集合として認めると、$M\in M \iff M \not\in M$ となって矛盾
では集合とは何か?
素朴な、ものの集まり、全体集合の部分集合では定義になっていない
直観的に理解しやすい定義は知られていない。
8.無限を数える:集合の濃度
集合 $A$ のサイズ(濃度)$|A|$の決め方有限集合なら要素数。無限集合は無限大?
2つの原則(直感)
① $A\subset B\to |A|\lt|B|$ ② $A$と$B$の要素が1対1対応すれば$|A|=|B|$
無限集合では、2つの直感があい反する
① 偶数⊂自然数 なので|偶数|$\lt$|自然数|
② $2n \Leftrightarrow n$ なので|偶数|=|自然数|
カントールは、①'$A\subseteq B \to |A|\le |B|$と②を採用し濃度を定義
パズル.無限の$1,2,\dots$号室を持つホテル無限がある。満室のある日
(1) 新たにお客が一人やってきた。支配人はどうしたか。
(2) 新たに無限人数の団体客がやってきた。支配人はどうしたか。
9.集合の濃度
定理.|A|<|2A|(濃度に上限なし!⇒ラッセルのパラドックス)略証.$f:A\to 2^A$に対し、$B=\{x|x\not\in f(x)\}=f(b)$と仮定すると矛盾。よって、$A$と$2^A$は1対1対応しない。
定理.|自然数|=|整数|=|有理数|=|有限長自然数列|=|有限長文字列|
<|2自然数|=|実数|=|無限長文字列|
略証.|自然数|=|有限長自然数列|:各項の和の小さい順に分類して並べる
(1),(2),(1,1),(3),(1,2),(2,1),(1,1,1),(4),(1,3),(2,2),(3,1),(1,1,2),(1,2,1),(2,1,1),(1,1,1,1),$\cdots$
パズル.稠密性と濃度比較
(1) 表現(有限長さ)を持つ実数はどのくらいあるか。
(2) 数直線上で有理数はどのように分布しているか。
アリストテレスの名辞論理:中世までの論理学
基本形 $A$は$B$($A,B\ne\emptyset$)| A型 | すべての$A$は$B$である | $A\subseteq B$ | I型 | ある$A$は$B$である | $A\cap B\ne\emptyset$ |
| E型 | すべての$A$は$B$でない | $A\cap B=\emptyset$ | O型 | ある$A$は$B$でない | $A-B\ne\emptyset$ |
三段論法
| 第1格 | 第2格 | 第3格 | 第4格 | |
| 前提1 | $A$は$B$ | $A$は$B$ | $B$は$A$ | $B$は$A$ |
| 前提2 | $B$は$C$ | $C$は$B$ | $B$は$C$ | $C$は$B$ |
| 結論 | $A$は$C$ | $A$は$C$ | $A$は$C$ | $A$は$C$ |
AEO型第1格の三段論法
すべての$A$は$B$である。
すべての$B$は$C$でない。
よってある$A$は$C$でない。
三段論法の覚え歌
AAA型第1格~OOO型第4格まで$256$通り、内$24$通りが妥当アリストテレスはこれらを第1格の妥当なAAA,EAE,AII,EIO型から同値な変形で証明した
中世論理学「名辞論理の3段論法をどう覚え適用できるか」
Barbara celarent darii ferioque prioris.
Cesare camestres festino baroco secundoe.
Tertia darapti disamis datisi felapton, bocardo ferison habet.
Quarta insuper addit bramantip camenes dimaris fesapo fresison.
(ウィキペディア)