正方行列
行列:数を縦横に並べたもの 正方行列:縦と横のサイズが等しい。
$[A]_{i,j}$:行列$A$の第$i$行第$j$列成分
和:$[A+B]_{i,j}=[A]_{i,j}+[B]_{i,j}
\left[\begin{array}{cccc}
0 & 1 & 2 \\
3 & 4 & 5 \\
6 & 7 & 8
\end{array}\right]
+
\left[\begin{array}{cccc}
0 & 3 & 6 \\
1 & 4 & 7 \\
2 & 5 & 8
\end{array}\right]
=
\left[\begin{array}{cccc}
0 & 4 & 8 \\
4 & 8 & 12 \\
8 & 12 & 16
\end{array}\right]$
積:$\displaystyle [A\cdot B]_{i,j}=\sum_{k=1}^n [A]_{i,k}\cdot [B]_{k,j}
\left[\begin{array}{cccc}
0 & 1 & 2 \\
\color{red}{3} & \color{red}{4} & \color{red}{5} \\
6 & 7 & 8
\end{array}\right]
\cdot
\left[\begin{array}{cccc}
\color{red}{0} & 3 & 6 \\
\color{red}{1} & 4 & 7 \\
\color{red}{2} & 5 & 8
\end{array}\right]
=
\left[\begin{array}{cccc}
5 & 14 & 23 \\
\color{red}{14} & 50 & 86 \\
23 & 86 & 149
\end{array}\right]$
グラフ\(G\)の隣接行列\(A_G\)
| \(A_{G_2}=\left[\begin{array}{ccc} 1 & 2 & 0 \\ 2 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right]\) |
| \(A_{G_2}^2=\left[\begin{array}{ccc} 5 & 2 & 2 \\ 2 & 5 & 0 \\ 2 & 0 & 1 \end{array}\right]\) |
\([A_G]_{i,k}\cdot [A_G]_{k,j}=頂点i,k,jを通る長さ2の路の数\) \(\displaystyle [A_G^2]_{i,j}=\sum_{k=1}^m [A_G]_{i,k}\cdot [A_G]_{k,j}=頂点iからjへの長さ2の路の数\)
グラフの隣接行列
\(\displaystyle [A_G^0]_{i,j}= \left\{\begin{array}{ll} 1 & i=jのとき\\ 0 & i\ne j のとき \end{array}\right. \hspace{6mm}=頂点iからjへの長さ0の路の数\) \(\displaystyle [A_G^n]_{i,j}=\sum_{k=1}^m [A_G^{n-1}]_{i,k}\cdot [A_G]_{k,j}=頂点iからjへの長さnの路の数\) \(\displaystyle A_G^*=\sum_{n=0}^\infty A_G^n ⇒ [A_G^*]_{i,j}=頂点iからjへの路の数\)注意.グラフに閉路があれば、\(A_G^*\)は発散する。
路の有無を表す行列
| p | q | p∧q | p∨q |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
ここで、\(+を\vee,\ \cdot を\wedge\)に置き換えると
\([B_G]_{ik}\wedge [B_G]_{kj}=頂点i,k,jを通る長さ2の路の有無\)
\(\displaystyle [B_G^2]_{i,j}=\bigvee_{k=1}^m [B_G]_{i,k}\wedge [B_G]_{k,j}=頂点iからjへの長さ2の路の有無\)
| \(B_{G_1}=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{array}\right],\ \) |
| \(B_{G_1}^2=\left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right]\) |
路の有無を表す行列
\(\displaystyle [B_G^0]_{i,j}= \left\{\begin{array}{ll} 1 & i=jのとき\\ 0 & i\ne j のとき \end{array}\right. \hspace{6mm}=頂点iからjへの長さ0の路の有無\) \(\displaystyle [B_G^n]_{i,j}=\sum_{k=1}^m [B_G^{n-1}]_{i,k}\cdot [B_G]_{k,j}=頂点iからjへの長さnの路の有無\)\(\displaystyle B_G^*=\sum_{n=0}^\infty B_G^n=\sum_{n=0}^{m-1} B_G^n\): 路があれば必ず辺の数が\(m-1\)以下の路がある。
最短距離を表す行列
各辺にその距離(非負の重み)を表す値(ラベル)が付いているグラフ\(G\)\([W_G]_{i,j}= \left\{\begin{array}{ll} 辺の距離の最小値 & 頂点iから頂点jへの辺があるとき\\ \infty & そうでないとき \end{array}\right.\)
ここで、\(+を\min,\ \cdot を+\)に置き換えると
\([W_G]_{ik}+[W_G]_{kj}=頂点i,k,jを通る長さ2の路の最短距離\)
\(\displaystyle [W_G^2]_{i,j}=\min_{k=1}^m ([W_G]_{i,k}+[W_G]_{k,j})=頂点iからjへの長さ2の路の最短距離\)
| \(W_G=\left[\begin{array}{cccc} \infty & 1 & \infty & 6 \\ 1 & \infty & 2 & 4 \\ \infty & 2 & \infty & 1 \\ 6 & 4 & 1 & \infty \end{array}\right],\ \) |
| \(W_G^2=\left[\begin{array}{cccc} 2 & 10 & 3 & 5 \\ 10 & 2 & 5 & 3 \\ 3 & 5 & 2 & 6 \\ 5 & 3 & 6 & 5 \end{array}\right]\) |
最短距離を表す行列
\(\displaystyle [W_G^0]_{i,j}= \left\{\begin{array}{ll} 0 & i=jのとき\\ \infty & i\ne j のとき \end{array}\right. \hspace{6mm}=頂点iからjへの長さ0の路の距離\) \(\displaystyle [W_G^n]_{i,j}=\min_{k=1}^m ([W_G^{n-1}]_{i,k}+[W_G]_{k,j})=頂点iからjへの長さnの路の最短距離\) \(\displaystyle W_G^*=\min_{n=0}^\infty W_G^n=\min_{n=0}^{m-1} W_G^n\): 路があれば必ず辺の数\(m-1\)以下の路がある。文字列の集合
連接:文字列をつなげる演算例.\(abc\cdot bca=abcbca\)
空列:長さ0の文字列\(\varepsilon\)
\(abc\varepsilon=\varepsilon abc=abc\)
文字列の集合に対する演算
連接 \(AB=\{xy|x\in A, y\in B\}\)
\(A^0=\{\varepsilon\}, A^1=A, A^{n+1}=AA^n\)
\(A^n はAに属す文字列を重複を許してn個つなげた文字列の集合\)
閉包 \(\displaystyle A^*=\bigcup_{n=0}^\infty A^n\)
\(A^* はAに属す文字列を重複を許してつなげた文字列の集合\)
路の集合を表す行列
各辺にラベル(文字)が付いているグラフ\([L_G]_{i,j}=頂点iから頂点jへの辺(のラベル)の集合\)
ここで、\(+を\cup,\ \cdot を連接\)に置き換えると
\([L_G]_{ik}[L_G]_{kj}=頂点i,k,jを通る長さ2の路の(ラベルの)集合\) \(\displaystyle [L_G^2]_{i,j}=\bigcup_{k=1}^m [L_G]_{i,k}[L_G]_{k,j}=頂点iからjへの長さ2の路の(ラベルの)集合\)
| \(L_G=\left[\begin{array}{ccc} \{a\} & \{b\} & \emptyset \\ \{a\} & \emptyset & \{b\} \\ \emptyset & \{a\} & \{b\} \end{array}\right],\ \) |
| \(L_G^2=\left[\begin{array}{ccc} \{aa,ba\} & \{ab\} & \{bb\} \\ \{aa\} & \{ab,ba\} & \{bb\} \\ \{aa\} & \{ba\} & \{ab,bb\} \end{array}\right]\) |
路の集合を表す行列
\(\displaystyle [L_G^0]_{i,j}= \left\{\begin{array}{ll} \{\varepsilon\} & i=jのとき\\ \emptyset & i\ne j のとき \end{array}\right. \hspace{6mm}=頂点iからjへの長さ0の路の(ラベルの)集合\) \(\displaystyle [L_G^n]_{i,j}=\bigcup_{k=1}^m [L_G^{n-1}]_{i,k}[L_G]_{k,j}=頂点iからjへの長さnの路の(ラベルの)集合\)\(\displaystyle L_G^*=\bigcup_{n=1}^\infty L_G^n\) の求め方は??
\(\displaystyle L_G^*\)の求め方
\([K_k]_{i,j}=頂点iから頂点jへの番号k以下の頂点を通る路の集合\)とすると、
\(K_0=L^0 \cup L\)
\([K_{k+1}]_{i,j}=[K_k]_{i,j} \cup [K_k]_{i,k+1}[K_k]_{k+1,k+1}^*[K_k]_{k+1,j}\)
\(L_G^*=K_m\)
が成り立つ。
\([L_G^*]_{i,j}\)は文字列(の単元集合)から、和、連接、閉包を組み合わせて表現できる。 このような集合を正規集合という。
例.簡単のため{,}を省略
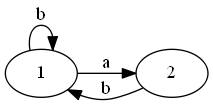
| \(L_G=\left[\begin{array}{cc} b & a \\ b & \emptyset \end{array}\right],\ \) |
| \(L_G^*=\left[\begin{array}{cc} (b\cup ab)^* & (b\cup ab)^*a \\ b(b\cup ab)^* & (bb^*a)^* \end{array}\right]\) |