チューリング機械
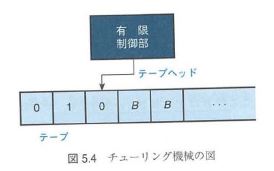
- 有限制御部
- テープ：いくらでも延長可能
- ヘッド：テープのマス目（セル）の読書き
動作：ヘッドが読み取る記号と有限制御部の内部状態から
- 有限制御部の状態を変える
- テープヘッドが見ているマスの記号を書きかえるか
ヘッドを右または左に動かす
加算を行う（間の$0$を消して詰める）TM(右表)の
時点表示列：$q_0110111\vdash 1q_010111\vdash 11q_00111$
$\vdash 111q_1111\vdash 1111q_111\vdash 11111q_11\vdash 111111q_1B$
$\vdash 11111q_21B\vdash 11111q_2BB$
ヘッドを右または左に動かす
万能チューリング機械
テープ上に書かれた動作表と入力から、その動きを模倣するチューリング機械が存在する
⇒プログラム記憶方式（ノイマン型）コンピュータ
言い換えると、任意のコンピュータをシミュレートできる万能プログラムが存在する。
注．一般にあるコンピュータをシミュレートするには、それより多くの記憶領域を必要とする。
チャーチ・チューリングのテーゼ
様々な計算モデルの計算能力が等しいことが証明された
- チューリング機械
- 帰納的関数
- λ計算
- ・・・
- コンピュータ
チャーチ・チューリングのテーゼ
これらのモデルで計算できる$\iff$コンピュータで計算できる$\iff$一般的な意味で計算できる
以後、コンピュータ(プログラム)に関する直感に基づいて議論を進める。
ただし、コンピュータの記憶装置は必要に応じていくらでも増やせるものとする。
パズル．コンピュータが(人工)知能だとみなせる条件は何か(チューリングテスト)。
計算不可能な問題
プログラムの停止問題：
入力：プログラム$P$とその入力$w$
出力：動作させたとき$P(w)$がいつかは停止(yes)するか否(no)か
定理．停止問題を解くプログラムは存在しない。
略証．停止問題を解くプログラム$H(P,w)$が存在するとする。$H(P,w)$から次の働きをするプログラム$H'(w)$が作れる。
%E3%81%AE%E5%9B%B3.JPG)
- $H'(w)$は停止しない$\iff H(w,w)=$yes
- $H'(w)=$no (停止する)$\iff H(w,w)=$no
$H'(H')=$no
$\iff H(H',H')=$no
$\iff H'(H')$は非停止
$\iff H(H',H')=$yes
$\iff H'(H')$は停止
となって、矛盾
ライスの定理
問題 := 問題例が無数にあり、答えがyes/noであるもの
自明な問題 := 答えがすべてyes、あるいはすべてnoである問題
プログラムの働きが等しい
:= 同じ入力に対し(停止しないことも含めて)同じ出力になる
プログラムの働きに関する問題
:= 働きが等しいプログラムに対しては答(yes/no)が等しくなる問題
定理．プログラムの働きに関する問題は自明なものを除いてすべて計算不能
ライスの定理の証明
定理．プログラムの働きに関する問題は自明なものを除いてすべて計算不能
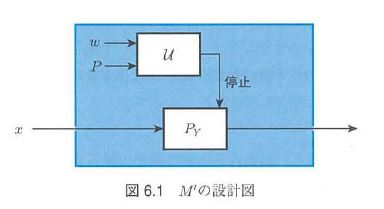
略証：自明でない問題$\mathcal{P}$を考え、それを解くプログラム$M$があるとする。今$M$は入力(プログラム)$P_Y$に対しYesを返し、決して停止しないプログラム$P_N$に対しNoを返すものとする。$M$から停止問題を解くプログラム$H(P,w)$が作れることを示す。$H$は入力として$(P,w)$を受け取ったら、図に示した$M'$のプログラムを作成し、$M$に読み込ませる。
（図中の$\mathcal{U}$は$(P,w)$を受け取り$P(w)$の動作を模倣する万能プログラム）
ここで$P(w)$が停止すれば$M'$は$P_Y$に(働きが)等しく、$P(w)$が停止しなければ$M'$は$P_N$に等しい。よって、$M'$を読み込んだ$M$は$P(w)$が停止するか否か判定できることになり、矛盾する。
解けない問題
| $i$ | $x_i$ | $y_i$ |
| 1 | 10 | 101 |
| 2 | 011 | 11 |
| 3 | 101 | 011 |
| $i$ | $x_i$ | $y_i$ |
| 1 | 1 | 111 |
| 2 | 10111 | 10 |
| 3 | 10 | 0 |
与えれた文字列の対(の集合)を並べて、同じ文字列対が作れるか。
ヒルベルトの第10問題
整係数の多変数多項式の方程式(ディオファントス方程式)が整数解を持つか。
$x^2+y^2-z^2=0$ の整数解は $(3,4,5),(5,12,13),\dots$
$(x^2+1)^3+(y^2+1)^3-z^3=0$ の整数解は存在しない
パズル．ポストの対応問題について、それぞれ解の有無を示せ。